Thursday, May 16, 2019

matematika wajib: SISTEM PERSAMAAN DAN PERTIDAKSAMAAN LINEAR DAN KUADRAT VARIABEL

7:41 PM

BAB IV

SISTEM PERSAMAAN DAN PERTIDAKSAMAAN LINEAR DAN KUADRAT VARIABEL

A. Sistem Persamaan Linear Dua Variabel(SPLDV)

Perhatikan kembali tentang materi Siatem Persamaan dan Pertidaksamaan Linear

Beberapa metode penyelesaiannya adalah sebagai berikut

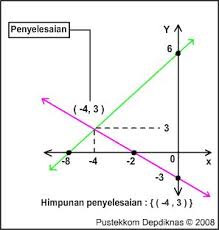
1. Dengan metode grafik

sebagaimana contoh berikut

dan

2. Dengan metode eliminasi dan atau substitusi

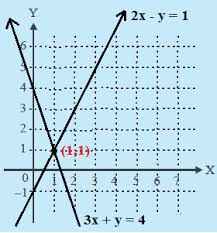
Perhatikan contoh poin b) di atas. Jika dua buah garis dengan persamaan $3x+y=4$ dan $2x-y=1$ , maka untuk mencari titik potong kedua garis tersebut kita dapat menggunakan metode eliminasi atau substitusi atau gabungan keduanya.

Misalkan kita ingin menggunakan metode gabungan eliminasi dan substitusi, maka

$\begin{matrix} 3x&+&y&=&4& \\ 2x& -&y&=&1&\\ \end{matrix}$

————————- +

$5x=5$

$x=1$

Selanjutnya nilai x=1 dimasukkan kesalah satu persamaan, misalkan ke 3x + y = 4, sehingga

$x=1\: \: \Rightarrow \: \: 3\left ( 1 \right )+y=4\: \: maka\: \: akan\: \: diperoleh \: \: y=1$

Coba cermati lagi ternyata titik potong kedua garis tersebut terletak di (1,1), tepat sebagaimana gambar grafik di atas.

B. Persamaan Kuadrat

Bentuk umum persamaan kuadrat adalah:

$\LARGE\boxed{ax^{2}+bx+c=0}$

$dengan \: \: a,b,c\: \epsilon \: \: \mathbb{R}\: \: dan\: \: a\neq 0$

Cara penyelesaian persamaan kuadrat di antaranya sebagai berikut

Persamaan kuadrat $\mathbf{ax^{2}+bx+c=0}\: \: dengan\: \: \mathbf{a,b,c\: \epsilon\: \mathbb{R}\: \: dan\: \: a\neq 0 }$ memiliki akar-akar $\mathbf{x_{1}\: \: dan\: \: x_{2}}$ di mana cara memperolehnya dapat menggunakan salah satu di antara 3 cara sebagaimana berikut; pemfaktoran, melengkapkan kuadrat sempurna dan formula abc.

1. Pemfaktoran

$\LARGE\boxed{ax^{2}+bx+c=a\left ( x-x_{1} \right )\left ( x-x_{2} \right )=0}$

untuk koefisien 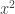$x^{2}$ lebih dari 1, maka ubahlah menjadi bentuk

$\LARGE\boxed{\frac{1}{a}\left ( ax-p \right )\left ( ax-q \right )=0}$

Contoh:

a. Tentukan akar-akar dari persamaan kuadrat $x^{2}-3x-10=0$

Jawab:

$x^{2}-3x-10=\left ( x+2 \right )\left ( x-5 \right )=0$ $\Leftrightarrow \: \: x=-2\: \: atau \: \: x=5$

b. Tentukan akar-akar dari persamaan $2x^{2}-3x-5=0$

Jawab:

$2x^{2}-3x-5=\frac{1}{2}\left ( 2x+2 \right )\left ( 2x-5 \right )=\left ( x+1 \right )\left ( 2x-5 \right )=0$ $\Leftrightarrow \: \: x=-1\: \: atau\: \: x=\frac{5}{2}$

2. Melengkapkan kuadrat sempurna

$ax^{2}+bx+c=0\: \: masing-masing\: \: ruas\: \: dibagi\: \: a$ ,

$x^{2}+\frac{b}{a}x+\frac{c}{a}=0$

$x^{2}+\frac{b}{a}x=-\frac{c}{a}\: \: kedua\: \: ruas\: \: ditambah\: \: \LARGE\boxed{(\frac{b}{2a})^{2}}$ ,

$x^{2}+\frac{b}{a}x+\left ( \frac{b}{2a} \right )^{2}=-\frac{c}{a}+\left ( \frac{b}{2a} \right )^{2}$ ,

$\left ( x+\frac{b}{2a} \right )^{2}=\Large{\frac{b^{2}-4ac}{4a^{2}}}$ ,

$\LARGE\boxed{\left ( x+\frac{b}{2a} \right )^{2}=\Large{\frac{b^{2}-4ac}{4a^{2}}}}$ .

Contoh:

Dengan melengkapkan kuadrat sempurna, tentukan akar-akar dari $2x^{2}-3x-5=0$

Jawab:

$2x^{2}-3x-5=0$ .

$\frac{2x^{2}}{2}-\frac{3x}{2}-\frac{5}{2}=\frac{0}{2}$ ,

$x^{2}-\frac{3}{2}x=\frac{5}{2}$ ,

$x^{2}-\frac{3}{2}x+\left ( \frac{3}{2\times 2} \right )^{2}=\frac{5}{2}+\left ( \frac{3}{2\times 2} \right )^{2}$ ,

$\Large{\left ( x-\frac{3}{4} \right )^{2}=\frac{5}{2}+\left ( \frac{3}{4} \right )^{2}}$ ,

$\Large{\left ( x-\frac{3}{4} \right )=\pm \sqrt{\frac{5}{2}+\frac{9}{16}}=\pm \sqrt{\frac{49}{16}}=\pm \frac{7}{4}}$ ,

$\Leftrightarrow \: \: \Large{x=\frac{3}{4}\pm \frac{7}{4}}$ ,

$\Leftrightarrow \: \: \Large{x=\frac{3+7}{4}=\frac{5}{2}\: \: atau\: \: x=\frac{3-7}{4}=-1}$ .

c. formula abc

Perhatikan kembali langkah pada melengkapkan kuadrat sempurna. formula abc sebenarnya pengembangan dari bagian langkah akhirnya.

$ax^{2}+bx+c=0\: \: masing-masing\: \: ruas\: \: dibagi\: \: a$ ,

$x^{2}+\frac{b}{a}x+\frac{c}{a}=0$

$x^{2}+\frac{b}{a}x=-\frac{c}{a}\: \: kedua\: \: ruas\: \: ditambah\: \: \LARGE\boxed{(\frac{b}{2a})^{2}}$ ,

$x^{2}+\frac{b}{a}x+\left ( \frac{b}{2a} \right )^{2}=-\frac{c}{a}+\left ( \frac{b}{2a} \right )^{2}$ ,

$\left ( x+\frac{b}{2a} \right )^{2}=\Large{\frac{b^{2}-4ac}{4a^{2}}}$ ,

$\Large{x+\frac{b}{2a}=\pm\sqrt{\frac{b^{2}-4ac}{4a^{2}}} }$ ,

$\LARGE\boxed{x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}}$

Contoh:

Dengan menggunakan formula abc, tentukan akar-akar dari $2x^{2}-3x-5=0$

Jawab:

$2x^{2}-3x-5=0\left\{\begin{matrix} a &=&2 \\ b &=&-3 \\ c &=&-5 \end{matrix}\right.$

$\Large{x=\frac{-(-b)\pm \sqrt{(-3)^{2}-4(2)(-5)}}{2(2)}}$ ,

$\Large{x=\frac{3\pm \sqrt{9+40}}{4}}$ ,

$\Large{x=\frac{3\pm 7}{4}}$ ,

$\Leftrightarrow \: \: x=\frac{5}{2}\: \: atau\: \: x=-1$ .

c. Sistem Persamaan Linear dan Kuadrat dua Variabel

Bentuk umum:

$\left\{\begin{matrix} y &= &ax &+&b \\ y &= &px^{2} &+&qx&+&r \end{matrix}\right.$

Langkah-langkah penyelesaian:

Substitusikan $y=ax+b$ ke bagian $y=px^{2}+qx+r$ , diperoleh $ax+b=px^{2}+qx+r$ . Sehingga kita mendapatkan $px^{2}+(q-a)x+(r-b)=0$
Nilai-nilai $x$ pada langkah pertama disubstitusikan ke $y=ax+b$ atau $y=px^{2}+qx+r$
Nilai $x$ yang ada tergantung dari nilai diskriminan D persamaan kuadrat , yaitu $\LARGE{D=\left ( q-a \right )^{2}-4p\left ( r-b \right )}$

Untuk rincian nilai D sebagai berikut:

$\begin{tabular}{|c|c|r|r|}\hline \emph{No}& \multicolumn{1}{|r|}{\emph{Jenis Nilai D}}&{\emph{penjelasan nilai D}}\\\hline 1&\boxed{D>0}&sistem persamaan mempunyai dua anggota dalam himpunan penyelesaiannya\\\hline 2&\boxed{D=0}&sistem persamaan mempunyai tepat satu anggota dalam himpunan penyelesaiannya\\\hline 3&\boxed{D<0}&sistem persamaan tidak memiliki anggota dalam himpunan penyelesaiannya\\\hline\end{tabular}$